Hypothesentests – Verfahren & Nullhypothese aufstellen
Ein Hypothesentest wird dazu benötigt, Vermutungen über Zusammenhänge in der Welt zu überprüfen. Auf Grundlage dieser Vermutungen werden Hypothesen aufgestellt.
Anhand eines statistischen Tests findest du heraus, wie wahrscheinlich die aufgestellte Hypothese ist. Demnach wird die Hypothese beibehalten oder verworfen.
Eine 100%ige Sicherheit, dass die Hypothese tatsächlich stimmt, kannst du jedoch nie erlangen. Es besteht immer eine kleine Möglichkeit, dass Ergebnisse nur durch Zufall entstanden sind.
Da es nicht möglich ist, die gesamte Population zu testen, wird stattdessen eine repräsentative Stichprobe verwendet. Auf Grundlage dieser Stichprobe werden Daten erhoben und später analysiert. Anhand der Resultate wird geschlussfolgert, wie die Ergebnisse auf die gesamte Population bezogen aussehen würden.
Schritte des Hypothesentests & Nullhypothese aufstellen
Eine Annahme und die daraus hervorgehenden Hypothesen sollten auf Erkenntnissen aus der Literatur oder wissenschaftlichen Theorien beruhen.
Befolge diese Schritte, um einen Hypothesentest durchzuführen:
1. Hypothesen aufstellen
Der erste Schritt des Hypothesentests ist es, eine Nullhypothese als Gegensatz zur eigentlichen Vermutung aufzustellen. Sie besagt, dass kein Zusammenhang oder Effekt besteht. Die Nullhypothese beschreibt also, dass mögliche gefundene Unterschiede nur durch Zufall entstanden sind.
Außerdem wird eine Alternativhypothese aufgestellt. Diese sagt genau das aus, was in der Studie überprüft werden soll, und repräsentiert somit die Vermutung, die aufgestellt wurde.
Nullhypothese: μ = μ0. Besagt, dass kein Zusammenhang besteht.
Alternativhypothese: μ ≠ μ0. Besagt, dass ein Zusammenhang besteht und nicht nur auf Zufall basiert.
μ steht für den Durchschnittswert in der Population. μ0 ist also der Durchschnittswert unter der Nullhypothese.
Nullhypothese H0: Du besitzt diese Fähigkeit nicht. Falls du das Sternzeichen von jemandem richtig rätst, ist dies nur Zufall.
Alternativhypothese H1: Du kannst die Sternzeichen tatsächlich erraten.
2. Datenerhebung
Um die aufgestellte Hypothese überprüfen zu können, sollten Daten erhoben werden. Hierbei wird eine Stichprobe von Teilnehmenden verwendet, da es nicht möglich ist, die gesamte Population in die Studie einzubeziehen.
Es ist wichtig, dass dein Studiendesign geeignet ist, um die Hypothese zu testen, und dass die Stichprobe repräsentativ für die Population ist. Ist dies nicht der Fall, sind die Ergebnisse weniger aussagekräftig oder sogar ungültig.
Nullhypothese H0: Du besitzt diese Fähigkeit nicht. Falls du das Sternzeichen von jemandem richtig rätst, ist dies nur Zufall.
Alternativhypothese H1: Du kannst die Sternzeichen tatsächlich erraten.
Um die Hypothesen zu überprüfen, führst du eine Studie durch, in der du per Zufallsprinzip Studierende an der Universität rekrutierst. Du gehst davon aus, dass die unterschiedlichen Sternzeichen in dieser Stichprobe gleichmäßig verteilt sind.
Nun rätst du die Sternzeichen jeder Person und dokumentierst im Nachhinein die tatsächlichen Sternzeichen der Teilnehmenden.
3. Statistischer Test
Nun sollte der korrekte statistische Test ausgewählt werden, um die Daten zu analysieren.
Welches der richtige Test ist, hängt davon ab, wie viele Variablen untersucht werden und welche Art von Variablen vorliegt. Außerdem ist es wichtig, ob Unterschiede innerhalb oder zwischen Gruppen gemessen werden und ob diese Gruppen voneinander unabhängig sind.
Hier erklären wir einige der meist verwendeten statistischen Tests:
Anhand des Tests wird ein p-Wert berechnet. Dieser gibt die Wahrscheinlichkeit an, dass die gefundenen Daten auftreten, wenn die Nullhypothese stimmt. Der p-Wert ist eines der wichtigsten Resultate des statistischen Tests, wenn du deine Hypothese prüfen möchtest.
4. Entscheiden, ob die Nullhypothese abgelehnt oder beibehalten wird
Basierend auf dem Ergebnis des statistischen Tests wird entschieden, ob die Nullhypothese abgelehnt oder beibehalten wird.
Der p-Wert gibt an, wie wahrscheinlich die Ergebnisse unter der Nullhypothese sind. Ist diese Wahrscheinlichkeit geringer als ein vorab gewähltes Signifikanzniveau, wird die Nullhypothese abgelehnt.
In den meisten Fällen ist dieses Signifikanzniveau 5 %. Die Nullhypothese wird demnach abgelehnt, wenn es weniger als 5 % wahrscheinlich ist, die gefundenen Resultate zu erhalten, wenn die Nullhypothese stimmt.
Wenn die Nullhypothese abgelehnt wird, sagen wir also: Die Ergebnisse hätten theoretisch durch Zufall entstehen können, doch die Wahrscheinlichkeit, dass diese Ergebnisse durch Zufall entstehen, ist sehr gering. Wir können uns deshalb relativ sicher sein, dass die Ergebnisse nicht durch Zufall entstanden sind.
Nullhypothese H0: Du besitzt diese Fähigkeit nicht. Falls du das Sternzeichen von jemandem richtig rätst, ist dies nur Zufall.
Alternativhypothese H1: Du kannst die Sternzeichen tatsächlich erraten.
Studiendesign: Du rätst die Sternzeichen der Studienteilnehmenden und fragst sie im Nachhinein nach dem wirklichen Sternzeichen.
Nehmen wir an, du rätst das Sternzeichen der ersten Person richtig. Wenn wir davon ausgehen, dass du keine solche Fähigkeit besitzt, dann gäbe es bei zwölf Sternzeichen trotzdem eine Chance von 8,333 %, dass du durch Zufall richtig liegst.
Die Wahrscheinlichkeit, dass du durch zufälliges Raten richtig liegst, ist noch zu hoch, um die Nullhypothese abzuweisen. Rätst du nun aber mehr und mehr Sternzeichen richtig, dann wird die Wahrscheinlichkeit geringer, dass du dies nur durch Zufall schaffst.
Wenn diese Wahrscheinlichkeit unter 5 % liegt, lehnen wir die Nullhypothese ab. Die Wahrscheinlichkeit, dass du all diese Sternzeichen durch Zufall richtig rätst, ist so gering, dass wir dir glauben müssen, diese Fähigkeit zu besitzen.
Beidseitige und einseitige Hypothesentests
Eine Hypothese kann beidseitig oder einseitig sein. Bei einer beidseitigen Hypothese ist noch nicht spezifiziert, in welche Richtung ein Zusammenhang erwartet wird. Es wird lediglich erwartet, dass ein Zusammenhang oder Effekt existiert.
Einseitige Hypothesen können linksseitig oder rechtsseitig sein. Die einseitigen Hypothesen konkretisieren bereits, ob erwartet wird, dass die Werte höher oder niedriger ausfallen als unter der Nullhypothese.
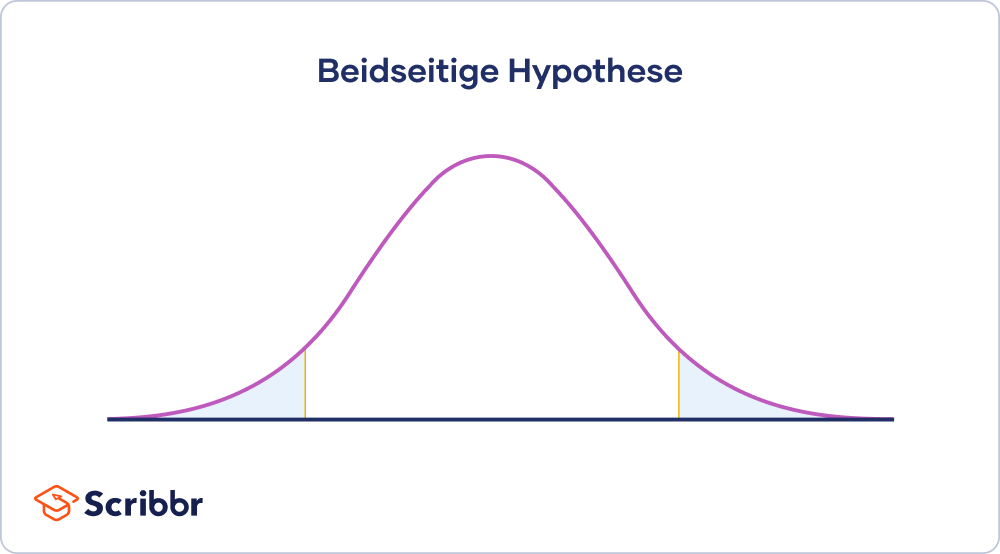
Beidseitiger Hypothesentest
Der beidseitige Hypothesentest ist ungerichtet. Das heißt, es gibt noch keine Annahme darüber, ob die Werte kleiner oder größer sind. Du vermutest nur, dass die Werte von der Nullhypothese abweichen. Es handelt sich deshalb um die Bereiche rechts und links in der Verteilung.
Deine Vermutung ist, dass Studierende sich unterschiedlich viel merken können, abhängig davon, ob sie gestresst sind oder nicht. Du spezifizierst noch nicht, ob du glaubst, dass sie sich weniger oder mehr merken.
Experiment: In deiner Studie lesen Studierende einen Text und müssen danach Fragen zu diesem beantworten. Im ungestressten Zustand beantworten Studierende bei diesem Test durchschnittlich 6,5 von 10 Fragen richtig.
Nullhypothese H0: μ = 6,5
Das durchschnittliche beibehaltene Wissen der Studierenden hängt nicht davon ab, ob sie gestresst sind oder nicht.
Alternativhypothese H1: μ ≠ 6,5
Das durchschnittliche beibehaltene Wissen der Studierenden ist höher oder niedriger, wenn sie gestresst sind.
μ steht für den Durchschnittswert.
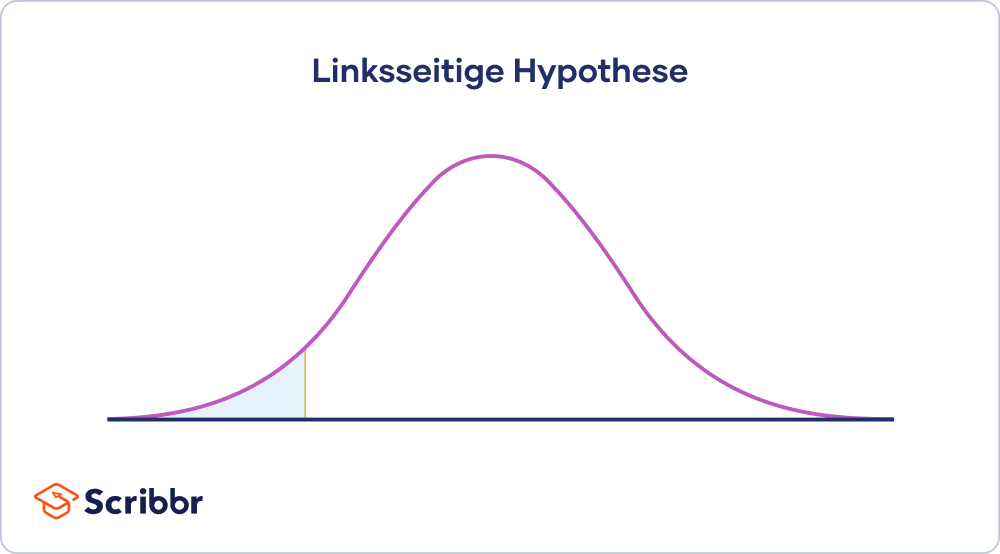
Linksseitiger Hypothesentest
Bei dem linksseitigen Hypothesentest geht es um die Werte links in der Verteilung. Die Alternativhypothese eines linksseitigen Hypothesentests besagt, dass die Werte geringer sind als in der Nullhypothese angenommen. Meist bedeutet dies, dass ein negativer Zusammenhang oder Effekt besteht.
Du vermutest, dass Studierende weniger Wissen beibehalten, wenn sie unter Stress lernen.
Experiment: In deiner Studie lesen Studierende einen Text und müssen danach Fragen zu diesem beantworten. Im ungestressten Zustand beantworten Studierende bei diesem Test durchschnittlich 6,5 von 10 Fragen richtig.
Nullhypothese H0: μ ≥ 6,5
Studierende merken sich durchschnittlich gleich viel oder mehr, wenn sie gestresst sind.
Alternativhypothese H1: μ < 6,5
Studierende merken sich durchschnittlich weniger, wenn sie gestresst sind.
μ steht für den Durchschnittswert.
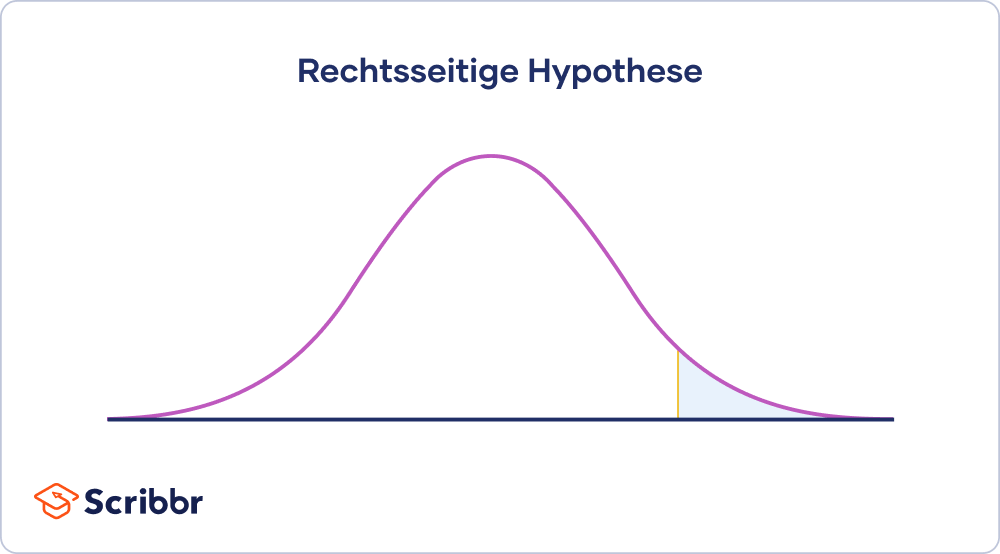
Rechtsseitiger Hypothesentest
Der rechtsseitige Hypothesentest fokussiert sich auf die Werte rechts in der Verteilung. Die Alternativhypothese eines rechtsseitigen Hypothesentests besagt, dass die Werte größer sind als unter der Nullhypothese angenommen. Meist besteht also ein positiver Zusammenhang oder Effekt.
Deine Vermutung ist, dass Studierende mehr Wissen beibehalten, wenn sie unter Stress lernen.
Experiment: In deiner Studie lesen Studierende einen Text und müssen danach Fragen zu deisem beantworten. Im ungestressten Zustand beantworten Studierende bei diesem Test durchschnittlich 6,5 von 10 Fragen richtig.
Nullhypothese H0: μ ≤ 6,5
Studierende merken sich durchschnittlich genau so viel oder weniger, wenn sie gestresst sind.
Alternativhypothese H1: μ > 6,5
Studierende merken sich durchschnittlich mehr, wenn sie gestresst sind.
μ steht für den Durchschnittswert.
Mögliche Fehler bei Hypothesentests
Im Allgemeinen solltest du bei den Schlussfolgerungen aus Hypothesentests vorsichtig sein. Manchmal findet die Studie zwar einen signifikanten Effekt – dies bedeutet jedoch nicht immer, dass du auf die gesamte Population schließen kannst.
Außerdem können beim Ablehnen oder Beibehalten der Hypothesen gewisse Fehler auftreten.
Fehler 1. und 2. Art
Bei Hypothesentests können zwei Fehler auftreten, die damit zusammenhängen, dass die Nullhypothese fälschlicherweise angenommen oder abgelehnt wird.
Der Fehler 1. Art liegt dann vor, wenn die Nullhypothese fälschlicherweise verworfen wird, obwohl sie wahr ist. Das heißt, es wird angenommen, dass es einen Effekt gibt, obwohl die Ergebnisse nur durch Zufall entstanden sind.
Ein Fehler 2. Art bedeutet, dass die Nullhypothese beibehalten wird, obwohl sie nicht wahr ist. Das heißt, dass es tatsächlich einen Effekt gibt, dieser jedoch nicht erkannt wurde.
| Wahrer Zustand | Entscheidung: H0 ablehnen | Entscheidung: H0 beibehalten |
|---|---|---|
| H0 stimmt | Fehler 1. Art | Korrekt |
| H0 stimmt nicht | Korrekt | Fehler 2. Art |
Häufig gestellte Fragen
- Wozu werden Hypothesentests benötigt?
-
Ein Hypothesentest wird dazu benötigt, Annahmen über die Welt zu überprüfen. Dazu werden Hypothesen aufgestellt, die anhand statistischer Tests überprüft werden.
- Was ist die Nullhypothese?
-
Die Nullhypothese ist das Gegenteil der Alternativhypothese und besagt, dass es keinen wirklichen Zusammenhang gibt. Mögliche Unterschiede sind demnach nur durch Zufall entstanden.
- Welchen Schritten sollte man beim Hypothesentest folgen?
-
Die vier Schritte des Hypothesentests sind: 1. Hypothesen aufstellen, 2. Daten sammeln, 3. Statistischen Test durchführen, 4. Entscheiden, ob die Nullhypothese abgelehnt oder beibehalten wird.
- Welche Arten von Hypothesentests gibt es?
-
Hypothesentests können einseitig oder beidseitig sein. Die einseitigen Tests können linksseitig oder rechtsseitig sein. Welcher Hypothesentest angebracht ist, hängt von der Forschungsfrage ab.
- Was für Fehler können beim Hypothesentest auftreten?
-
Im allgemeinen solltest du mit Verallgemeinerungen auf die gesamte Population (oder Grundgesamtheit) vorsichtig sein. Außerdem können beim Hypothesentest die Fehler 1. und 2. Art auftreten.
Diesen Scribbr-Artikel zitieren
Wenn du diese Quelle zitieren möchtest, kannst du die Quellenangabe kopieren und einfügen oder auf die Schaltfläche „Diesen Artikel zitieren“ klicken, um die Quellenangabe automatisch zu unserem kostenlosen Zitier-Generator hinzuzufügen.
Hasselbusch, L. (2023, 24. April). Hypothesentests – Verfahren & Nullhypothese aufstellen. Scribbr. Abgerufen am 10. Februar 2025, von https://www.scribbr.at/statistik-at/hypothesentests/
